100 дней на машинное обучение | Day60 нерешительности, XGBoost

машинное обучение

XGBoost — это интегрированный алгоритм машинного обучения., который можно использовать для различных задач, таких как регрессия, классификация и сортировка, и широко используется в соревнованиях по машинному обучению и в промышленных областях. Успешные примеры включают в себя: классификацию текста веб-страницы, прогнозирование поведения клиентов, анализ настроений, прогнозирование рейтинга кликов по рекламе, классификацию вредоносных программ, классификацию элементов, оценку рисков и крупномасштабное прогнозирование процента отсева онлайн-курсов.

XGBoost — одна из самых глубоких моделей для начинающих. Она соединяет точки знаний, такие как дерево решений, бустинг и GBDT. Всем настоятельно рекомендуется попробовать. В этой статье я будуПроисхождение и преимущества XGBoost, принцип модели и вывод оптимизации, анализ параметров модели XGBoost, пример настройки параметров, визуализация XGBoostПредставьте XGBoost и так далее. Напоминаю, XGBoost — это усовершенствование на базе GBDT.Для прочтения этой статьи необходимо иметь определенное представление о GBDT.Незнакомые студенты могут прочитать предыдущую статью:Получите машинное обучение за 100 дней | Day58 Введение в машинное обучение: жесткий демонтаж GBDT

Происхождение и преимущества XGBoost

В моделировании данных часто используется метод Boosting, объединяющий сотни или тысячи древовидных моделей с низкой точностью классификации в прогностическую модель с высокой точностью. Модель будет повторяться непрерывно, создавая новое дерево с каждой итерацией. Однако, когда набор данных сложный, могут потребоваться тысячи итераций, что приведет к огромным вычислительным узким местам.

В ответ на эту проблему XGBoost (eXtreme Gradient Boosting), разработанный доктором Ченом Тяньци из Вашингтонского университета, реализует параллельное построение деревьев регрессии с помощью многопоточности на основе C++ и улучшает исходный алгоритм Gradient Boosting, тем самым значительно улучшая скорость обучения модели и точность прогноза.

Основные преимущества XGBoost заключаются в следующем.:

1. GBDT использует информацию о производной только первого порядка во время оптимизации, XGBoost использует производные как первого, так и второго порядка, а также поддерживает пользовательские функции потерь при условии, что функция потерь может быть производными первого и второго порядка;

2. Добавлен регулярный член для контроля сложности модели и предотвращения переобучения;

3. Опираясь на практику случайного леса, он поддерживает выборку столбцов (случайный выбор признаков), что может не только уменьшить переобучение, но и сократить вычисления;

4. При поиске наилучшей точки сегментации реализован метод аппроксимации, а также учитывается обработка разреженных наборов данных и пропущенных значений, что значительно повышает эффективность алгоритма;

5. Поддержка параллелизма;

6. Алгоритм приближенной гистограммы для эффективного создания точек-кандидатов на сегментацию;

7. В реализации алгоритма сделано множество оптимизаций, что значительно повышает эффективность работы алгоритма.При недостатке памяти используются идеи блокировки, предварительной выборки, сжатия и многопоточной кооперации.

Принцип и оптимизация модели XGBoost

XGBoost на самом деле является своего рода GBDT или аддитивной моделью и алгоритмом прямой оптимизации.

аддитивная модельДругими словами, сильный классификатор формируется путем линейного добавления ряда слабых классификаторов. Общая комбинация выглядит следующим образом:FM(x;P)=∑m=1nбетаmh(x;am)F_M(x;P)=\sum_{m=1}^n\beta_mh(x;a_m)в,h(x;am)h(x;a_m)является слабым классификатором один за другим,ama_m- оптимальный параметр, изученный слабым классификатором,бетаmβ_м— доля слабого обучения в сильных классификаторах, а P — всеальфаmα_мибетаmβ_мКомбинация. Эти слабые классификаторы добавляются линейно, чтобы сформировать сильный классификатор.

шаг впередТо есть в процессе обучения классификатор, созданный в следующем раунде итераций, обучается на основе предыдущего раунда. То есть его можно записать в таком виде:Fm(x)=Fm−1(x)+бетаmhm(x;am)F_m (x)=F_{m-1}(x)+ \beta_mh_m (x;a_m)

Как выглядит модель XGBoost?

y^i=∑k=1Kfk(xi),fkеF\hat{y}_i = \sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F}

  • где К - количество деревьев.
  • ffдерево регрессии,f(x)=wq(x)f(x)=w_{q(x)}, удовлетворять(q:Rm→T,wеRT)(q: R^m \rightarrow T, w \in R^T)
  • q представляет структуру каждого дерева, которое сопоставляет экземпляр обучающей выборки с соответствующим конечным индексом.
  • Т - количество листьев на дереве.
  • Каждый соответствует независимой древовидной структуре q и весу листа w.
  • F\mathcal{F}это функциональное пространство, состоящее из всех деревьев регрессии.

В отличие от деревьев решений, каждое дерево регрессии содержит непрерывную оценку на каждом листе, которую мы используем для представления оценки на i-м листе. Для данного экземпляра выборки мы используем правила принятия решений для дерева (заданное q), чтобы классифицировать его по листьям, и вычисляем окончательный результат путем суммирования оценок соответствующих листьев (заданных w) предсказанного значения.

Изучение XGBoost

Чтобы изучить эти наборы функций в этой модели, мы будемРегуляризованная целевая функция для минимизации:

obj(θ)=∑inl(yi,y^i)+∑k=1KОм(fk)\text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)

в:ll— функция потерь, есть 2 общих:
Функция квадратичных потерь:l(yi,yi)=(yi−yi)2л(уи,у^я)=(у_я-у^я)2
Функция потерь логистической регрессии:l(yi,yi)=yiln⁡(1+e−y^i)+(1−yi)ln⁡(1+ey^i)l(yi,y^i)=y_i\ln\left(1+e^{-\hat{y}_i}\right)+\left(1-y_i\right)\ln\left(1+e^{\hat{y}_i}\right)

Ом(Θ)Ом (Θ): термин регуляризации, используемый для наказания сложных моделей во избежание переобучения обучающих данных. Обычно используемые закономерности - это регулярность L1 и регулярность L2:
Закономерность L1 (лассо):Ом(w)=λ∣∣w∣∣1Ω ( ш ) = λ∣∣w∣∣_1
L2 регулярность:Ом(w)=λ∣∣w∣∣2Ω ( w ) = \lambda ||w||^2

Следующий шаг — изучить целевую функцию, каждый раз сохранять исходную модель неизменной и добавлять новую функцию.ffв нашу модель.

\шляпа{у}_i^{(1)} &= f_1(x_i) = \шляпа{у}_i^{(0)} + f_1(x_i)\\ \шляпа{у}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ &\dots\\ \hat{y}_i^{(t)} &= \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)\end{split}$$, где $\hat{y_i}^{ ( t)}$ — прогноз i-го экземпляра на t-й итерации, нам нужно добавить дерево $f_t$, а затем минимизировать следующую целевую функцию:

\begin{split}\text{obj}^{(t)} & = \sum_{i=1}^n l(y_i, \hat{y}i^{(t)}) + \sum{i=1}^t\Omega(f_i) \ & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + \mathrm{constant}\end{split}

Предполагая, что функция потерь использует квадрат потерь $l(yi,y^i)=(y_i−y^i)2$ , приведенная выше формула далее записывается как:

\begin{split}\text{obj}^{(t)} & = \sum_{i=1}^n (y_i - (\hat{y}i^{(t-1)} + f_t(x_i)))^2 + \sum{i=1}^t\Omega(f_i) \ & = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + \mathrm{constant}\end{split}

Теперь определим приблизительную целевую функцию, используя разложение Тейлора: $\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{( t- 1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + \mathrm{constant}$, где: $$\begin{split}g_i &= \partial_{\шляпа{у}_i^{(t-1)}} l(y_i, \шляпа{у}_i^{(t-1)})\\ h_i &= \partial_{\шляпа{ y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})\end{split}$$ $g_i, h_i$ - потери соответственно Первый и градиенты второго порядка по функции. Для тех из вас, кто забыл основы, давайте, кстати, вернемся к **формуле Тейлора**.Формула Тейлора — это формула, которая использует информацию о функции для описания значения рядом с ней. Его первоначальное намерение состоит в том, чтобы использовать полиномы для аппроксимации ситуации с функцией вокруг определенной точки. Базовый вид функции $f(x)$ в точке $x_0$ выглядит следующим образом

\begin{align*} f(x) &= \sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \&= f(x_0) +f^{1}(x_0)(x-x_0)+ \frac{f^{2}(x_0)}{2}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \end{align*}

Существует еще один распространенный способ записи, $x^{t+1} = x^t + \Delta x$, разложение Тейлора $f(x^{t+1})$ в $x^t$ , мы получаем : $$\begin{align*} f(x^{t+1}) &= f(x^t) +f^{1}(x^t)\Delta x+ \frac{f^{2}( x^t)}{2}\Delta x^2 + \cdots \end{align*}$$ Теперь давайте избавимся от констант и вернемся к нашей новой **целевой функции**: $$\sum_ {i= 1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)$$ определить $I_j = \{i|q(x_i) =j\ }$ — множество экземпляров листа j. $\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$ Введите обычный член и разложите целевую функцию:

\begin{split}\text{obj}^{(t)} &\approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\ &= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T\end{split}$$

Это выглядит немного сложно, пусть:Gj=∑iеIjgiG_j = \sum_{i\in I_j} g_i,Hj=∑iеIjhiH_j = \sum_{i\in I_j} h_i, приведенная выше формула упрощается до:

obj(t)=∑j=1T[Gjwj+12(Hj+λ)wj2]+γT\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T

В приведенной выше формулеwjw_jнезависимы друг от друга,Gjwj+12(Hj+λ)wj2G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2является квадратным термином. для определенной структурыq(x)q(x), мы можем рассчитать оптимальный весwj*w_j^{\ast}:

\begin{split}w_j^\ast &= -\frac{G_j}{H_j+\lambda}\\ \end{split}

будетwj*w_j^{\ast}Подводя к приведенной выше формуле, расчетные потери оптимального решенияobj*{obj}^*:

Obj^{\ (t)} &=\sum_{j=1}^T \left(G_jw_j + \frac{1}{2} (H_j + \lambda) w_j^2\right) +\gamma T\\ &=\sum_{j=1}^T \left(- \frac{G_j^2}{H_j+\lambda} + \frac{1}{2} \frac{G_j^2}{H_j+\lambda} \right ) +\gamma T\\ &=- \frac{1}{2}\sum_{j=1}^T \left({\color{red}{\frac{G_j^2}{H_j+\lambda}} } \right) +\gamma T \tag{2-8} \end{align*}$$ ${obj}^*$ можно использовать в качестве оценочной функции для измерения качества древовидной структуры $q(x)$. Теперь, когда у нас есть способ измерить, насколько хорошо дерево, давайте теперь обратимся ко второму вопросу оптимизации XGBoost: как выбрать, на какую функцию и значение функции разделить, чтобы мы получили наименьшую функцию потерь? Показатели выбора функции XGBoost и выбора точки отсечки определяются следующим образом:

\begin{align*} gain=\underbrace{\frac{G_L^2}{H_L+\lambda}}{оценка левого узла} + \ underbrace {\ frac {G_R ^ 2} {H_R + \ lambda}}{оценка правого узла}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{перед сегментацией}-\gamma \конец{выравнивание*}

### Как разделить? Можно использовать точный жадный алгоритм для перечисления всех возможных разделов по всем функциям. ![](https://p3-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/2d3de1eee13c41abbf590096b54b8a0f~tplv-k3u1fbpfcp-zoom-1.image) - попытаться разделить дерево решений на основе текущего узла, по умолчанию score score=0 , G и H являются суммой производных первого и второго порядка узлов, которые в данный момент необходимо разделить. - Для признаков с номерами k=1,2...K:$G_L=0, H_L=0$ - Расставить выборки по признаку k от меньшего к большему, брать по очереди i-й образец, по очереди вычислять текущий образец и поместить его в левое поддерево. Затем просуммировать первую и вторую производные левого и правого поддеревьев: $G_L = G_L+ g_{ti}, G_R=G-G_L$ $H_L = H_L+ h_{ti}, H_R=H- H_L$ — попытаться обновить наибольший результат: $$score = max(score, \frac{1}{2}\frac{G_L^2}{H_L + \lambda} + \frac{1}{2}\frac {G_R^2}{H_R+\lambda} - \frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+ \lambda} -\gamma)$$ - Разделение поддеревьев на основе разделения признаки и собственные значения, соответствующие наибольшему счету. - Если максимальный балл равен 0, текущее дерево решений установлено, вычислить $w_{tj}$ всех листовых областей, получить слабый ученик $h_t(x)$, обновить сильного ученика $f_t(x)$, и введите следующий один раунд итераций слабого ученика.Если максимальный балл не равен 0, продолжайте пытаться разделить дерево решений. ### Основной вывод (сокращенная версия) Ниже приведена упрощенная версия основного вывода XGBoost, которая удобна для ознакомления и использования учащимися.

\начать{выравнивать*} \начать{массив}{л} \text{Модель прогнозирования:}F(x)=\sum_{i=1}^Tw_if_i(x)\ \text{Целевая функция: }obj^t=\sum_{i=1}^NL(y_i,F_i^t(x_i))+\Omega(f_t)\

\because obj^t=\sum_{i=1}^NL(y_i,F_i^t(x_i))+\Omega(f_t)\\
~~~~~~~~~=\sum_{i=1}^NL(y_i,F_i^{t-1}(x_i)+w_tf_t(x_i))+\Omega(f_t)\\
\text{由泰勒公式: }f(x+\Delta x)\thickapprox f(x)+\nabla f(x)\Delta x+\frac{1}{2}\nabla^2 f(x)\Delta x^2\\
\therefore obj^t\thickapprox\sum_{i=1}^N[L(y_i,F_i^{t-1}(x_i))+\nabla _{F_{t-1}}L(y_i,F_i^{t-1}(x_i))w_tf_t(x_i)\\
~~~~~~~~~~~~~~~\frac{1}{2}\nabla _{F_{t-1}}^2L(y_i,F_i^{t-1}(x_i))w_t^2f_t^2(x_i)]+\Omega(f_t)\\
\text{令 $g_i=\nabla _{F_{t-1}}L(y_i,F_i^{t-1}(x_i))$}\\
~~~~~~h_i=\nabla _{F_{t-1}}^2L(y_i,F_i^{t-1}(x_i))\\
~~~obj^t\thickapprox \sum_{i=1}^N[L(y_i,F_i^{t-1}(x_i))+g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)\\
\because L(y_i,F_i^{t-1}(x_i)) \text{ 是常量}\\
\therefore \text{目标函数:}\\
~~~obj^t=\sum_{i=1}^N[g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)+C\\
\text{用叶子节点集合以及叶子节点得分表示 ，每个样本都落在一个叶子节点上:}\\ 
f_t(x)=m_q(x),~~m\in R^T,~~q:R^d\rightarrow\{1,2,3,...,T\}\\
\Omega(f_t)=\gamma T+ \frac{1}{2}\lambda \sum_{i=1}^Tm_j^2,\\
\text{$T$ 是第 $t$ 棵树叶子结点总数}\\
\text{$m_j$ 是第j个叶子结点的权重}\\
\text{定义第 $j$ 个叶子节点所在的样本为 $I_j=\{i|j=q(x_i)\}$}\\
\text{新的目标函数:}\\
obj^t=\sum_{i=1}^N[g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)\\
~~~~~~~=\sum_{i=1}^N[g_iw_tm_q(x_i)+\frac{1}{2}h_iw_t^2m_q^2(x_i)]+\gamma T+ \frac{1}{2}\lambda \sum_{i=1}^Tm_j^2\\
~~~~~~~=\sum_{j=1}^T[(\sum_{i \in I_j}g_i)w_tm_j+\frac{1}{2}(\sum_{i \in I_j}h_iw_t^2+\lambda )m_j^2]+\gamma T\\
\text{令： $G_j=\sum_{i \in I_j}g_i$ , $H_j=\sum_{i \in I_j}h_i$ }\\
obj^t=\sum_{j=1}^T[G_jw_tm_j+\frac{1}{2}(H_jw_t^2+\lambda)m_j^2]+\gamma T\\
\text{对二次函数优化问题:}\\
m_j^*=-\frac{G_j^2w_t}{H_jw_t^2+\lambda}\\
obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2w_t^2}{H_jw_t^2+\lambda}+\gamma T\\
\text{令 $w_t=1$ ：}\\
m_j^*=-\frac{G_j}{H_j+\lambda}\\
obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gamma T\\
\text{所以当我们新增一个切分点增益为:}\\
gain=\underbrace{\frac{G_L^2}{H_L+\lambda}}_{左节点得分}+\underbrace{\frac{G_R^2}{H_R+\lambda}}_{右节点得分}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{切分前得分}-\gamma
\end{array}
\end{align*}
$$


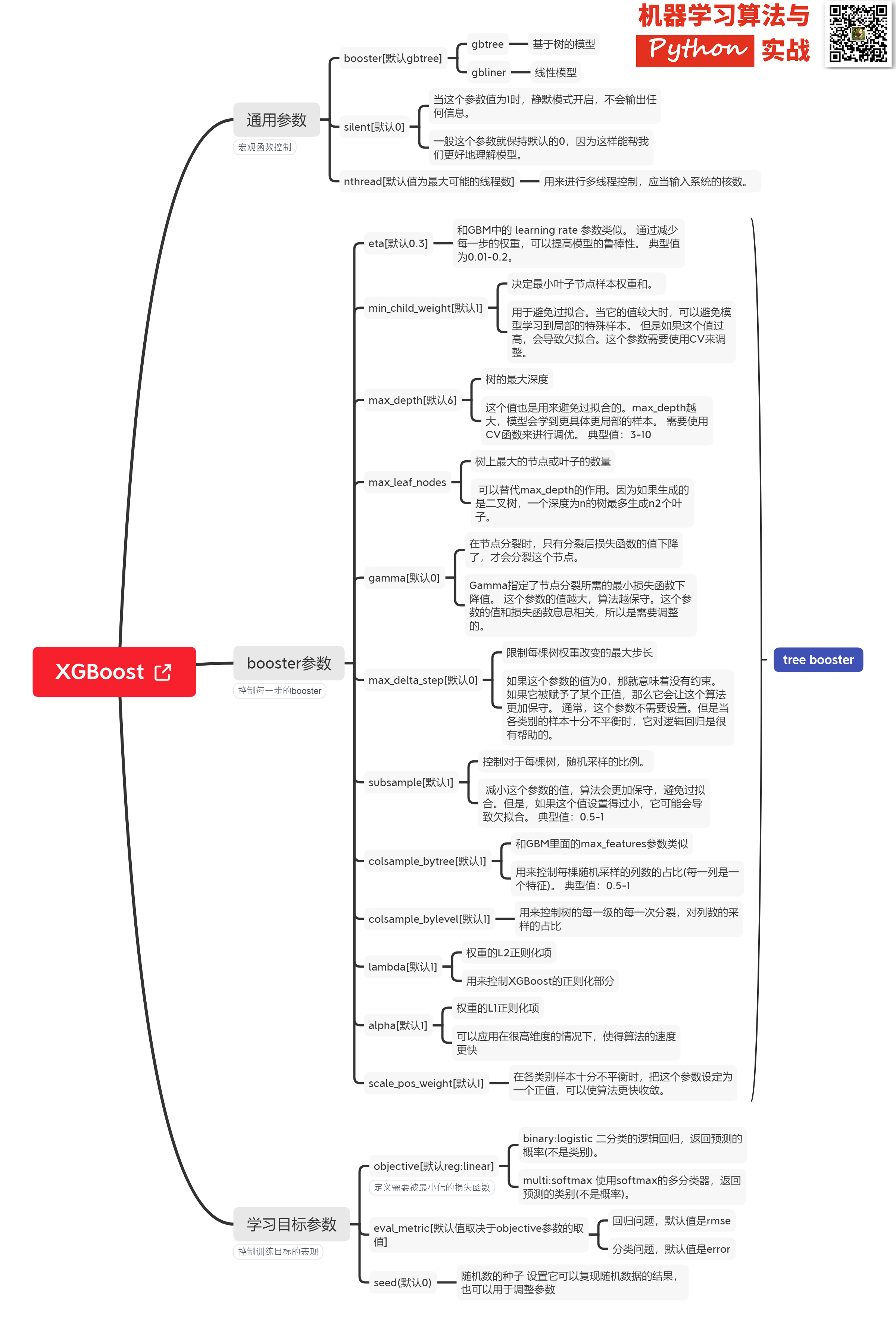
### Xgboost@sklearn模型参数解析
XGBoost的实现有原生版本，同时也有Scikit-learn版本，两者在使用上有一些微差异，这里给出xgboost.sklearn 参数解释。XGBoost使用**key-value**字典的方式存储参数：
```
#部分重要参数
params = {
    'booster': 'gbtree',
    'objective': 'multi:softmax',  # 多分类的问题
    'num_class': 10,               # 类别数，与 multisoftmax 并用
    'gamma': 0.1,                  # 用于控制是否后剪枝的参数,越大越保守，一般0.1、0.2这样子。
    'max_depth': 12,               # 构建树的深度，越大越容易过拟合
    'lambda': 2,                   # 控制模型复杂度的权重值的L2正则化项参数，参数越大，模型越不容易过拟合。
    'subsample': 0.7,              # 随机采样训练样本
    'colsample_bytree': 0.7,       # 生成树时进行的列采样
    'min_child_weight': 3,
    'silent': 1,                   # 设置成1则没有运行信息输出，最好是设置为0.
    'eta': 0.007,                  # 如同学习率
    'seed': 1000,
    'nthread': 4,                  # cpu 线程数
}
```
![xgboost完整参数解析](https://my-wechat.oss-cn-beijing.aliyuncs.com/XGBoost_20201205091216.png)

篇幅原因，调参实例及XGBoost可视化且听下回分解。  
如有收获，还请不吝给个**在看、收藏、转发**
## 参考
https://www.cnblogs.com/pinard/p/10979808.html  
https://www.biaodianfu.com/xgboost.html
https://www.zybuluo.com/vivounicorn/note/446479
https://www.cnblogs.com/chenjieyouge/p/12026339.html
Категории