Математическое моделирование рассматривается в конце семестра, и с целью подведения итогов пишется блог.В основном основное внимание уделяется построению модели примера и реализации части кода.Читатели могут исправить недостатки.
Использование набора инструментов дифференциального решения Matlab
Предположим, что корабль А в начале координат запускает ракеты по кораблю В в точке А(1, 0) по оси абсцисс, а головная часть ракеты всегда нацелена на корабль В. Если корабль В движется с максимальной скоростьюv0(Постоянная) При движении по прямой линии, параллельной оси Y, скорость ракеты равна 5v0, найти уравнение кривой работы ракеты. Какое расстояние пройдет корабль Б, прежде чем в него попадет ракета?
Построение модели и решение
1. Аналитический метод
Установление модели: пусть положение ракеты в момент времени t равно P(x(t), y(t)), а корабль B находится в точке Q(1,V0t), из вопроса (головка ракеты всегда направлена на корабль Б), касательная ракеты в точке p дуги движенияy'=1−xv0t−yкоторыйv0t=(1−x)y'+y(1)А из смысла названия (скорость ракеты в 5 раз больше скорости корабля) есть:∫0x1+y'2dx=5v0t(2)Имеются уравнения (1) и (2), дифференциально-дифференциальное уравнение можно получить в виде:(1−x)y''=511+y'2(3)Уравнение начального значения:y(0)=0,y'(0)=0, который может быть решен Matlab:y=−85(1−x)54+125(1−x)56+245
2. Численное решение
Преобразуя приведенное выше уравнение в уравнение первого порядка, мы можем установитьy1=y,y2=y', подставляя в (3), чтобы получить{y1'=y2y2'=511+y12/(1−x)Решить с помощью Matlab:
%定义函数
function dy=eq1(x,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=1/5*sqrt(1+y(1)^2)/(1-x);
end
调用
x0=0;
xf=0.9999;
[x,y]=ode15s('eq1',[x0 xf],[0 0]);
plot(x,y(:,1),'-')
hold on
y=0:0.01:2;
plot(1,y,'*')
Как видно из рисунка, ракета попала в Корабль Б примерно в точку (1,0,2).
3. Параметрическое уравнение
Полагая, что вышеуказанный вывод остается неизменным, на этом основании скорость ракеты устанавливается равнойw, то в точке P находятся:(dtdx)2+(dtdy)2=w2(1)При этом ракета всегда нацелена на Корабль Б, то есть вектор скорости ракеты параллелен вектору положения Корабля Б, поэтому имеются:
\ frac {\ mathrm {d} x} {\ mathrm {d} t} \\ \ frac {\ mathrm {d} y} {\ mathrm {d} t} \ end {array} \ right) = \ lambda \ left(\begin{array}{l} Xx \\ Yy \end{array}\right), \quad \lambda>0(2)$$ будет $$\left\{\begin{array}{l} \ frac {\ mathrm {d} x} {\ mathrm {d} t} = \ frac {w} {\ sqrt {(Xx) ^ {2} + (Yy) ^ {2}}} (Xx) \\ \ frac {\ mathrm {d} y} {\ mathrm {d} t} = \ frac {w} {\ sqrt {(Xx) ^ {2} + (Yy) ^ {2}}} (Yy) \ end { array}\right.(3)$$ Предположим, что скорость корабля B равна 1, тогда w=5, X=1, Y=t, параметр траектории ракеты в это время: $$\left\{ \begin{массив} {l} \frac{\mathrm{d} x}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+(ty)^ {2}}} (1-x) \\ \frac{\mathrm{d} y}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+ (ty)^{ 2}}}(ty) \\ x(0)=0, y(0)=0 \end{array}\right.$$ Решение Matlab: ```php function dy=eq2(t ,y) dy= нули(2,1); dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(ty(2))^2) ; dy(2) =5*(ty(2))/sqrt((1-y(1))^2+(ty(2))^2); end % call [t,y]=ode45(' eq2',[0 2],[0 0]); Y=0:0,01:2; plot(1,Y,'-') удерживается на plot(y(:,1),y(:,2), '*') ` `` 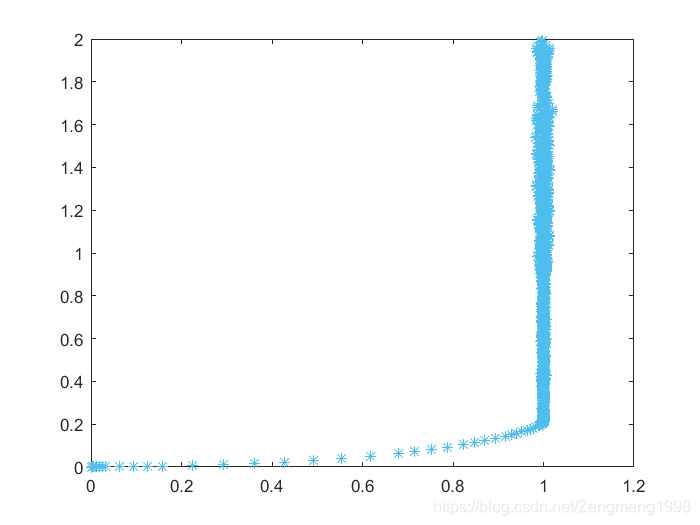 Как видно из рисунка, ракета окончательно попала в цель примерно на (1, 0,2). Здесь мы пытаемся использовать идею дихотомии, чтобы получить более точный ответ, ... tf=0,21 - это доступное изображение решения: , чтобы получить более точный ответ.